合并K个有序数组(python)

题目是: 给定K个有序数组,将它们合并成一个数组并且有序, 需要考虑时间复杂度.

这也是leetcode上的第23道题,由合并两个数组延生而来.

K个数组合并

这里做个假设, 有序数组的个数为 L

所有数组中, 最长数组的长度为 N, 每个数组中的元素个数可以不等

很正常的会想到写二层for循环相邻两两进行合并,但时间复杂度肯定过不去

可以使用最小堆, python中很少情况会想到使用堆, 开始还以为python中没有, 顺便研究了下heap,具体思路为:

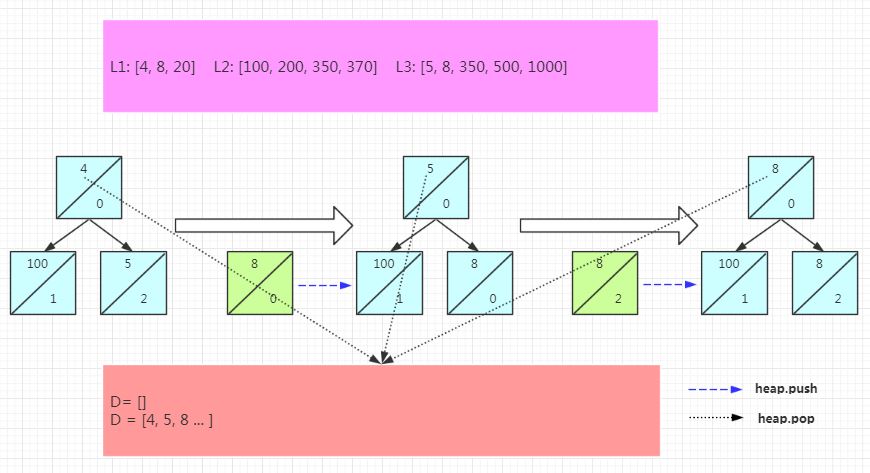
1. 维护一个最小堆, 堆的个数等于链表个数, 为L
2. 维护一个新链表,为D
3. 初始化堆中的元素为每个链表的第一个元素
4. 由最小堆的特性,堆的最顶层元素为最小值,每次取该最小值并记录该最小值所在有序链表的索引
5. 将该最小值添加到D中
6. 再把该最小值所在的链表的下一个元素入堆(如果存在的话)
7. 循环4-6直到所有元素都已添加到D中

import heapq
from collections import deque

def list_merge(*lists):
    #入参判断, 这里直接pass
    #将所有链表转化为deque,方便使用popleft获取链表的最左元素及根据索引返回该索引对应的剩余链表
    queues = [queue for queue in map(deque, lists)]
    heap = []
    #初始化链表,该链表中的元素为元组, 各个链表的第一个元素及链表所在索引
    for i, lst in enumerate(queues):
        heap.append((lst.popleft(), i))
    #将链表转换成最小堆
    heapq.heapify(heap)
    #链表: 用于存放每次获取的堆顶层元素
    result = []
    
    while heap:
        #将堆顶层元素出堆
        value, index = heapq.heappop(heap)
        #将顶层元素追加
        result.append(value)
        #根据索引获取对应链表的剩余元素
        if queues[index]:
             #如果存在下一个元素,则将该元素及索引入堆
            heapq.heappush(heap, (queues[index].popleft(), index))
    return result


print list_merge(*[[4, 8, 20], [100, 200, 350, 370], [5, 8, 350, 500, 1000]])

通过索引来获取对应数组的下一个元素, 使用的非常巧妙

这里主要使用到了heapq跟deque,大家可以到官网查看这两个的用法

复杂度分析

• 时间复杂度: 由于每个元素都需要读取一次, 即最大次数为L*N, 将每一个元素插入最小堆中的复杂度为O(logL),即总的复杂度为O(L*NlogL)
• 空间复杂度为: 维护最小堆的大小,即 O(L)

在实际中的运用

在分布式任务聚合后需要按照时间顺序统一排序的场景下会有这个需要,linux下也有一些实现,可参照这篇文章

参考文章:

• https://docs.python.org/3/library/heapq.html
• https://docs.python.org/3/library/collections.html#deque-objects
• https://leetcode.com/problems/merge-k-sorted-lists/solution/
• 合并N个有序链表与FQ公平调度

转载请注明原作者: 周淑科(https://izsk.me)

---